When determining the formal charge of a molecule such as CoCl2 (phosgene gas), you need to know the number of valence electrons for each atom and the Lewis structure of the molecule.
Look up each atom in the periodic table of elements to determine the number of valence electrons.
Remember that two electrons go in the first s shell, two electrons in the second s shell, six electrons in the first p shell, etc. As a reminder: 1s(^2)2s(^2)2p(^6)3s(^2)3p(^6)
Adjust for charge. If the molecule is an ion, add or subtract one or more electrons overall to account for the final charge.
- When determining the formal charge of a molecule such as CoCl2 (phosgene gas), you need to know the number of valence electrons for each atom and the Lewis structure of the molecule.
- If the molecule is an ion, add or subtract one or more electrons overall to account for the final charge.
For CoCl2 (Phosgene gas): C = 4; O = 6; Cl = 7. The molecule is not ionised and has a neutral charge. Therefore, the total amount of valence electrons is 4 + 6 + (7x2) = 24.
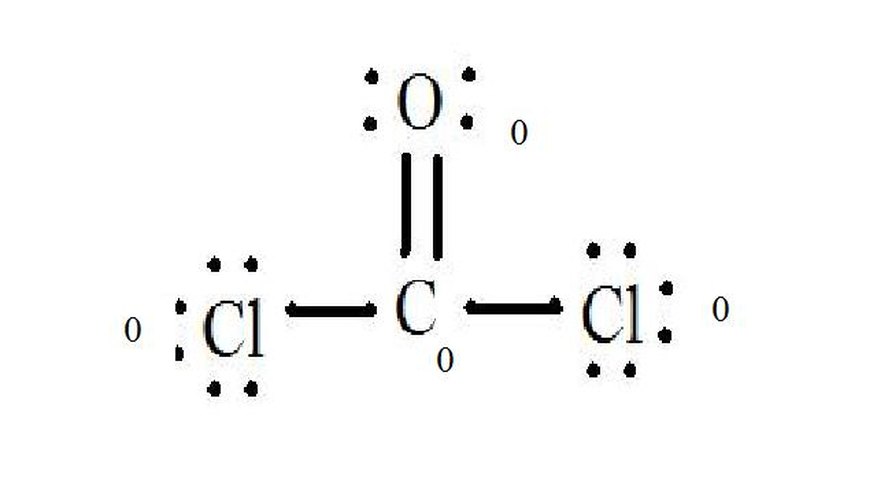
See the diagram for the Lewis structure of CoCl2 (phosgene gas). The Lewis structure represents the most stable and probable structure for a molecule. Atoms are drawn with paired valence electrons; bonds are formed between lone electrons to satisfy the octet rule.
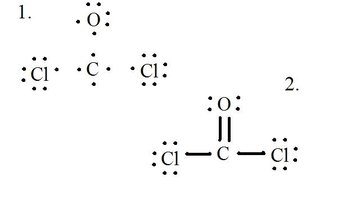
Draw each atom and its valence electrons, then form bonds as needed.
The chloride atoms share single bonds with the carbon molecule, while the oxygen atom forms a double bond with carbon. Each atom in the final structure satisfies the octet rule and has eight valence electrons allowing for molecular stability.
- See the diagram for the Lewis structure of CoCl2 (phosgene gas).
- Each atom in the final structure satisfies the octet rule and has eight valence electrons allowing for molecular stability.
Count the lone pairs of each atom in the Lewis structure. Assign each atom one electron from each bond in which it participates. Add these numbers together. In CoCl2: C = 0 lone pairs plus 4 electrons from bonds = 4 electrons. O = 4 electrons from lone pairs plus 2 electrons from bonds = 6 electrons. Cl = 6 electrons from lone pairs plus 1 electron from a bond with C = 7 electrons.
Subtract the sum from the number of valence electrons in the unbonded atom. The result is the formal charge for that atom. In CoCl2: C = 4 valence electrons (v.e.) in unbonded atom minus 4 assigned electrons in Lewis structure (L.s.) = 0 formal charge O = 6 v.e. - 6 L.s. = 0 formal charge Cl = 7 v.e. - 7 L.s. = 0 formal charge
- Subtract the sum from the number of valence electrons in the unbonded atom.
- In CoCl2: C = 4 valence electrons (v.e.)
Write these charges next to the atoms in the Lewis structure. If the overall molecule has a charge, enclose the Lewis structure in brackets with the charge written outside the brackets in the upper right corner.
WARNING
Calculating the formal charge for molecules containing transition metals can be tricky. The number of valence electrons for transition metals will be those outside the noble gas-like core.