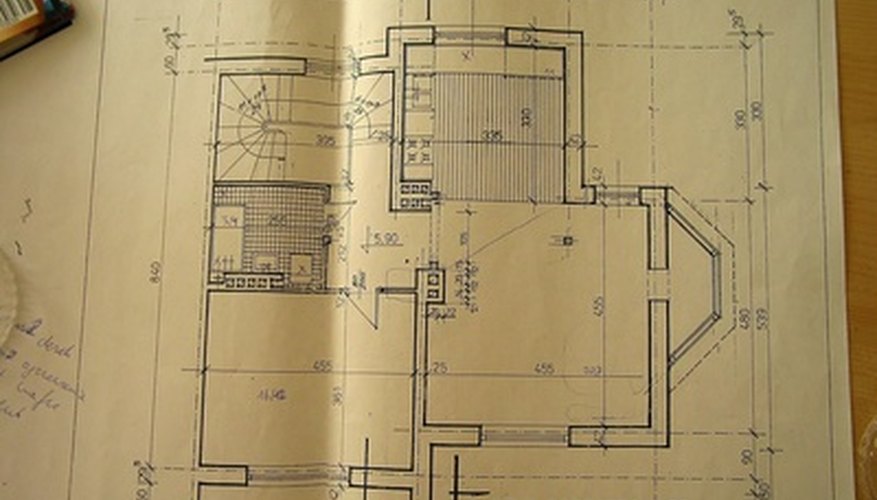
A floor plan is a bird's-eye view of each floor of a building abstracted as though there is no roof and only a few basic structural elements in the building, such as walls and doors. Because stairs are so common in architectural floor plans, there are shorthands and symbols for stairs that make drawing them a simple and straightforward task. The main difficulties are drawing to scale, using the correct measurements for the stair, and making the design decisions about where the stairs should go.
Decide where the stairs should go in the floor plan. Consider the layout of the building and which places are convenient to move between floors.
Determine the distance the stairs have to travel upward. This action plays a huge role in determining how long the stairs have to be because the risers and treads of the stairs are always the same height and width and the stairs have to be comfortable to walk up or down. For example, a room with a 9-foot ceiling would have stairs that have risers that are 7 inches tall and treads that are a standard 11 inches, calling for 15 treads. This translates into a bit less than a 12-foot long stairway.
- A floor plan is a bird's-eye view of each floor of a building abstracted as though there is no roof and only a few basic structural elements in the building, such as walls and doors.
- This action plays a huge role in determining how long the stairs have to be because the risers and treads of the stairs are always the same height and width and the stairs have to be comfortable to walk up or down.
Convert your stairway length into the scale you're using for your floor plan. For example, if 1/4 inch on the drawing equals 1 foot in real life--a common scale for blueprints--a 12-foot stairway would be 3 inches long in the drawing.
Draw a rectangle of the right scaled dimensions to the stairway you wish to build. Draw an arrow parallel to the long side of the rectangle and inside the rectangle. Point the arrow in the direction the stairwell is leading in the building. The arrow always points from the base of the stairs to the top.
- Convert your stairway length into the scale you're using for your floor plan.
- Draw a rectangle of the right scaled dimensions to the stairway you wish to build.
Draw parallel lines dividing the rectangle into the treads. Draw about seven treads and then draw a diagonal line dividing the rectangle and cutting through a couple of the treads. Insert a jagged line into the diagonal line so that it looks like a seismograph reading. This is a symbol that indicates a stairwell and is a shorthand method for drawing stairs in a floor plan.
Repeat steps 1 through 5 to create a circular stairs except instead of drawing a rectangle draw a circle with your compass and use your architect's rectangle to draw the treads, which in a circular stairs look like slices of a pie.