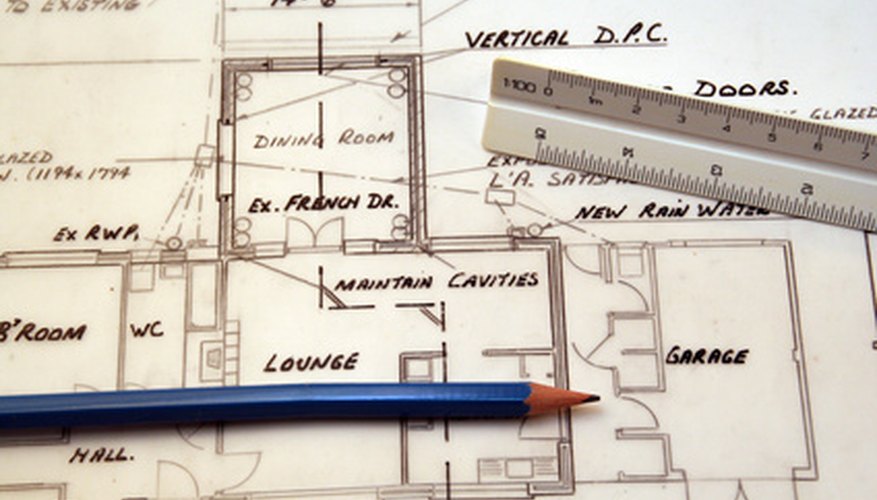
The purpose of a technical drawing is to clarify an idea and to translate that idea into a common graphical language. Manufacturers of a product apply their literacy in this language to interpret a technical drawing so they can build the particular structure represented and defined by it. Through technical drawings, drafting professionals show manufacturers the exact size, shape and location of each part of a structure. Technical drawings fulfil their purpose of idea translation through the application of a variety of methods and visual conventions.
Measurements
While a technical drawing communicates the shape of each part of a proposed structure with a visual representation, the exact size and position of the structure must come from measurements, which drafters call "dimensions." Among the dimensions you'll see on the front view of a house, for example, are those that convey the front view's complete width. A drawing will show that dimension as a line under or above the image of the house's front view. The line extends from the left to the right side of the house. At the centre of the line the drafter will enter the dimension for the house's width. The dimension will be in feet, meters, or whatever unit the production crew needs to build the house.
- While a technical drawing communicates the shape of each part of a proposed structure with a visual representation, the exact size and position of the structure must come from measurements, which drafters call "dimensions."
- A drawing will show that dimension as a line under or above the image of the house's front view.
Conveying Tolerances
Tolerance is the range of dimensions that a structure and its components can take. For example, a technical drawing may show that the entrance to a doghouse has the following width dimension: "14 inches, +/- 1/4 inch." This dimension is communicating that the doghouse's entrance can measure 14 inches across, give or take a quarter of an inch. Production crews need drafters to specify tolerances for a number of reasons, the foremost being that it's nearly always impossible to make a part to an exact size or position. Most objects expand or contract from heat or other environmental factors.
- Tolerance is the range of dimensions that a structure and its components can take.
- This dimension is communicating that the doghouse's entrance can measure 14 inches across, give or take a quarter of an inch.
Projection Views
Projection views are easiest to understand by example. The top projection view of a house will show you the roof of the house, while the front projection view will show you the front door and windows. A technical drawing can depict these views as orthographic or perspective. The front perspective view of a railroad track will show the tracks' rails as converging toward each other. By contrast, the front orthographic view of those same tracks will show you something like a pair of two large "I"s, which represent the cutaway view of the two rails of the track.
- Projection views are easiest to understand by example.
- The front perspective view of a railroad track will show the tracks' rails as converging toward each other.
Expressing Form and Structure
Technical drawings achieve their purpose of conveying a structure's shape through graphical two-dimensional (2-D) images. An example of an image that conveys a form is a circle, which can represent many real-world objects, such as a sphere, or the top view of a drinking glass. A drafter will draw the side view of a drinking glass as a simple rectangle with its top edge removed. Note that an actual drinking glass would not look like the rectangle or circle, but these graphics are conventions commonly understood to represent real-life forms.
- Technical drawings achieve their purpose of conveying a structure's shape through graphical two-dimensional (2-D) images.
- An example of an image that conveys a form is a circle, which can represent many real-world objects, such as a sphere, or the top view of a drinking glass.
Lettering
Production crews require technical drawings to be as clear as possible. Drafters thus undergo training to make the numbers and letters they write immediately legible. This training includes exactly what strokes of a pencil are needed to produce each letter of the alphabet, and each number. The characters that result from these strokes are usually in a typeface called Gothic, which doesn't have serifs (the small curves that Times New Roman, Courier and other fonts place on "S" and other characters).
- Production crews require technical drawings to be as clear as possible.
- Drafters thus undergo training to make the numbers and letters they write immediately legible.